LS 13320 XR – Particle Size Analysis Application Note
Introduction
Particle size analyses have become indispensable in many areas and applications of mechanical process engineering. On the basis of the results, it is possible, inter alia, to:
• Control product quality
• Detect possible process fluctuations
• Optimize the production process
• Determine the influence of machine and company size
The measurement should be carried out as quickly as possible and without great effort with regard to sampling and sample preparation. Furthermore, users demand high reproducibility of the results of particle size analysis and Operation should be intuitive, with operator influence eliminated as much as possible. In addition, the particle size analysis system must withstand the rigors of everyday use.
Beckman Coulter has met these challenges with the LS 13 320 XR particle size analyser. This field report summarizes the first experiences with the LS 13 320 XR.
Measurement results when taking sample
In mechanical process engineering, the temporal progress of a process is of ten monitored, or the change of a process parameter and its effect on the product is monitored, on the basis of random samples taken. This is the case, for example, with comminution or classification processes. A fast, uncomplicated, reproducible particle size analysis is of primary importance.
Reproducibility of results for repeated measurement of a sample
When random samples are taken without sample division, the particle sizes can be significantly scattered by repeated measurements of individual samples. Even repeated particle size analyses of the same sample can show strong fluctuations of the sum distribution or distribution density values. The reasons for this can be manifold. Using ultrasound, for example, fragile particles can be comminuted or, due to different orientations of the particles to the measuring plane, different diffraction spectra can be generated due to irregular particle shapes, which in turn can be assigned different particle sizes.
The statistics use confidence intervals to indicate the fluctuations around the true value µ. The size of the confidence intervals is influenced by the confidence level S, to be determined beforehand, and the number of samples k taken.
The arithmetic mean x is calculated from the samples according to this relationship:
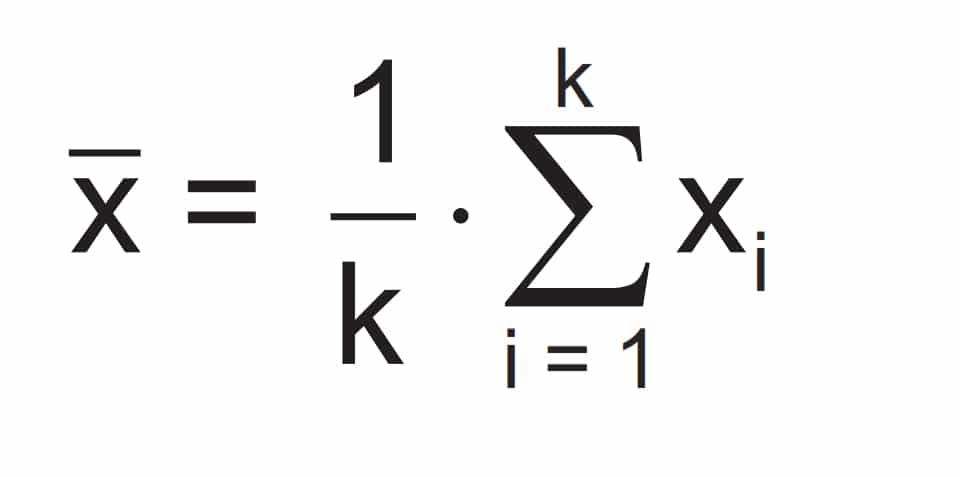
With a confidence level of S = 95% (with 100 measured values, 95 lie within the confidence interval limits) and a sample number k = 3, a student factor t = 4.30 results. With the empirical standard deviation s, the confidence interval around the true mean µ follows:
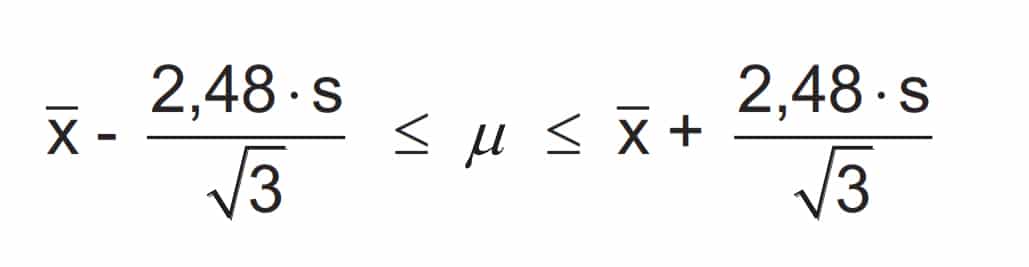
Figure 1 shows the determined particle size distribution densities q3(x) with the corresponding confidence intervals for a limestone flour sample with triple repeated measurement.
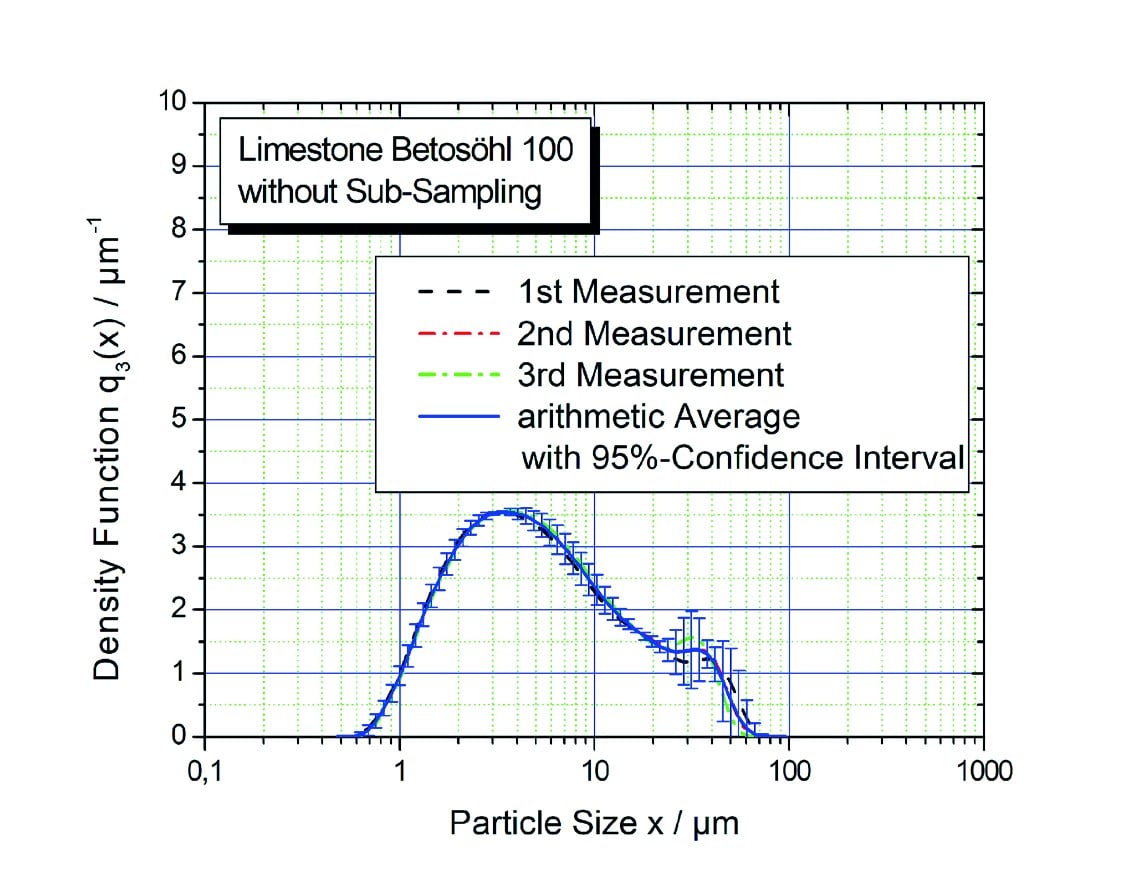
Figure 1: Particle size distribution densities q3(x) of limestone powder Be-tosöhl 100 for multiple measurements of a mixed sample without sample division.
It can be seen that the confidence intervals in the fine range are very narrow and that larger confidence intervals only occur with larger particle sizes x > 20 µm. The causal fluctuations can be traced back to different orientations of larger particles during passage of the measuring volume, which generate different diffraction patterns.
Reproducibility of results when measuring several pooled samples
Another important aspect in particle size analysis of mixed samples with multiple sampling without sample division and preparation is the reproducibility of results. This is relevant, for example, if the homogeneity of a polymer mass product such as expandable EPS granulate is to be tested. Figure 2 shows the results of the particle size analysis with the LS 13 320 XR for three samples of EPS granules type P326.
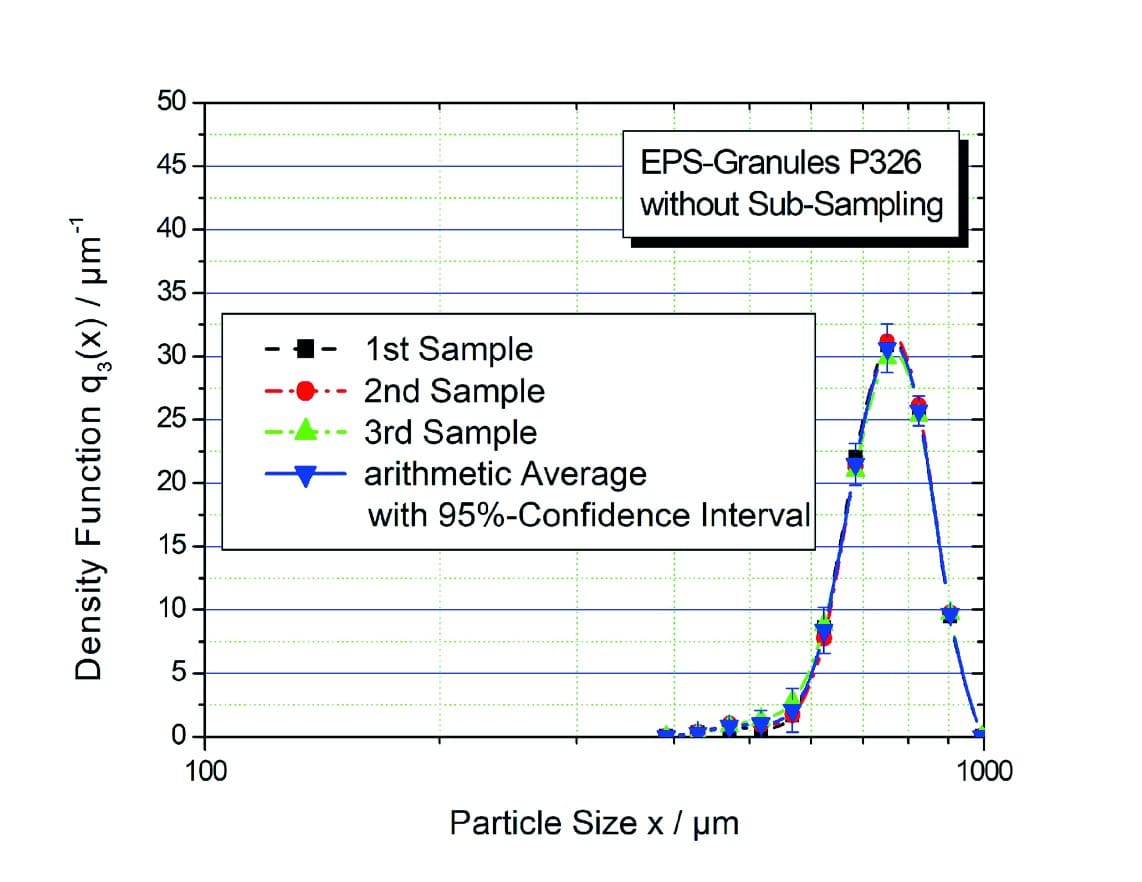
Figure 2: Particle size distribution densities q3(x) of expandable polystyrene granulate P326 when measuring 3 mixed samples without sample division.
The illustration clearly shows that even without prior sample division there is sufficient homogeneity of the EPS particle sizes, as the confidence interval of the true mean is small for all measured values. It can also be concluded that there is no segregation due to differences in particle size and/or shape. In addition, there are no significant differences in solids density, which could also cause segregation.
Presentation of the results of a particle size analysis with the LS 13 320 XR
There are different opinions about the presentation form of the results of particle size analyses as sum distribution or distribution density. In principle, both display variants express the same result, but the distribution density of ten allows a deeper insight into possible imperfections of separation processes.
An example of fine limestone flour of the Betosöhl 100 type is shown in Figure 3. The test material was produced by multistage comminution with fractionation by air separation.
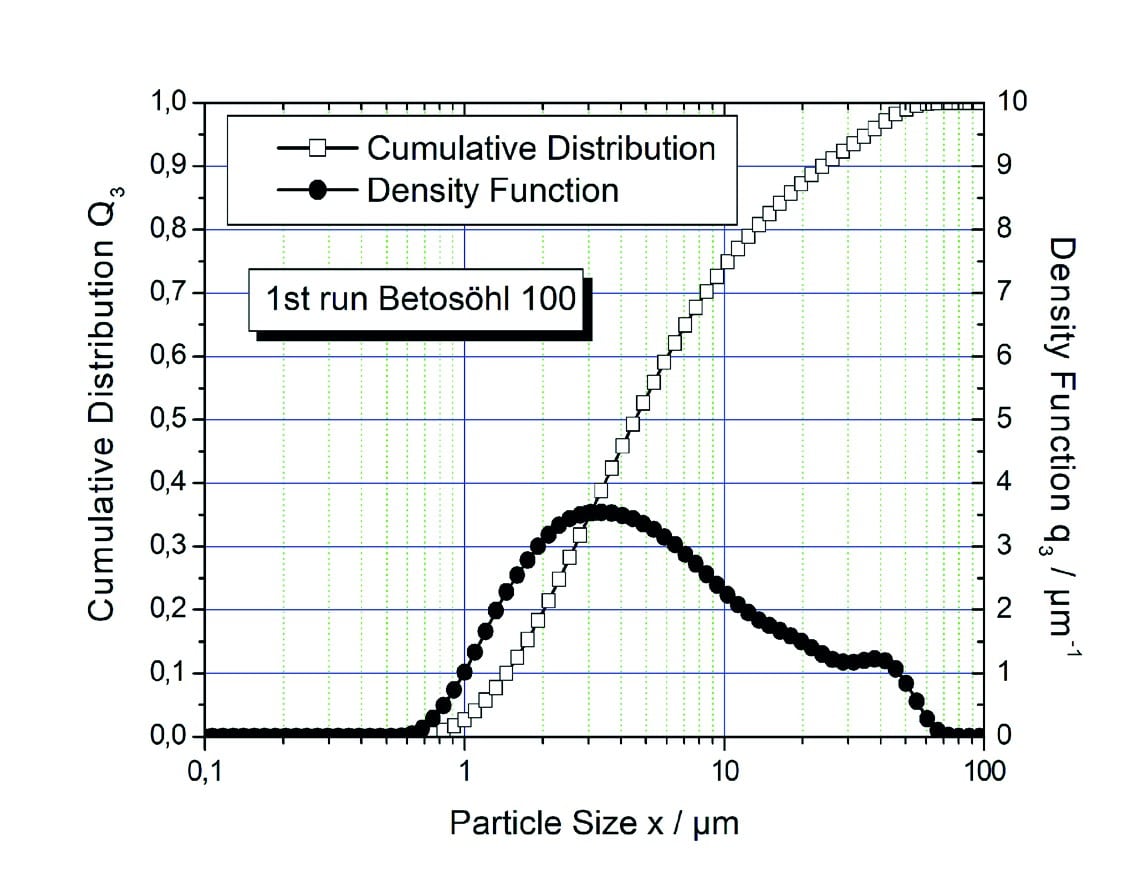
Figure 3: Particle size distribution densities q 3(x) and particle size sum distribution Q3(x) of limestone powder Betosöhl 100.
While the sum distribution increases almost monotonously, and only on closer inspection a bimodality characterized by two turning points is recognizable, the latter is clearly visible in the representation as distribution density by two local maxima. Only by means of the distribution density can it be clearly recognized that the classification or sifting was not very precise.
Bottom Line
The LS 13 320 XR is characterized by easy handling and good reproducibility of the measurement results. The operation of the particle size analyser is intuitive via the menu and does not pose a major challenge for the user. In addition, the LS 13 320 XR impresses with its high resolution of the measurement results, which ensures good reproducibility even in the absence of sample division but sufficient sample size and low segregation tendency.
