
The Coulter Principle for Outlier Detection in Highly Concentrated Solutions
The Coulter Principle for Outlier Detection in Highly Concentrated Solutions – Particle Characterisation Application Note
Abstract
This application note will benefit chemical and material manufacturers concerned about micron and submicron particle contamination. Outliers are a common problem in many industrial applications. Outliers can be defined as particles that are significantly larger or smaller than the main particle size distribution, but which occur in a much lower frequency than the main particle size. As a simple example, consider a hypothetical sample that contains 1,000,000 particles with a diameter of exactly 10 microns and only one particle with a diameter of 40 microns mixed together. In this sample, the 40-micron particle would be considered an outlier to the main distribution.
Detection of outliers presents a special problem in particle characterisation, since most instruments are designed to report on the average size of a population, and often miss outliers with lower frequency of occurrence. For particle characterisation by light scattering, the data can also be highly skewed due to a few large outliers. Larger outliers may dominate the signal because light scattering scales with (radius of particle) to the sixth power. This application note demonstrates the ability of the Coulter Principle to detect outliers in suspensions of highly concentrated small particles.
Concept of “Outlier”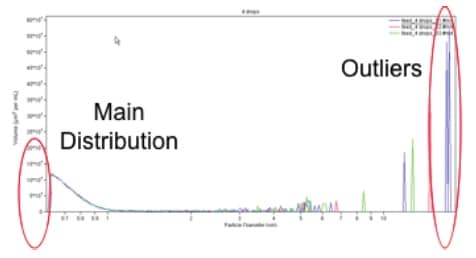
Introduction
Particle characterisation techniques generally fall into one of two categories: “ensemble” techniques (multiple particles are analysed simultaneously), or “discrete” techniques (individual particles are measured one at a time). Ensemble techniques, especially light scattering or laser diffraction, are poorly suited for outlier detection, since they are designed to give highly accurate and reproducible information about the entire population of particles, rather than individual particles. Consider the scenario described previously—an instrument based on light scattering would report the mean diameter as 10 microns and would likely miss the largest particle, because the light scattered by that single particle would generate significantly less signal than the million particles in the main distribution.
In contrast, discrete techniques are excellent for outlier detection since particles are analysed individually. A discrete instrument would report the mean diameter of 10 microns that the ensemble technique described, but also note that the population consisted of 1,000,001 particles, one of which had a diameter of 40 microns.
This type of information can be of great importance in fields ranging from pharmaceuticals to abrasives manufacturing. If a specification is ever set for zero tolerance—or very low tolerance—of particles above a certain size, then the only suitable way to confirm samples are acceptable is to use a discrete particle analysis approach.
This application focuses on an industrially relevant example: large particles in highly concentrated solutions of Chemical Mechanical Planarisation (CMP) slurries. The Coulter Principle will be introduced first, followed by a demonstration using a Multisizer 4 instrument.
Coulter Principle IntroductionThe Coulter Principle is a discrete technique particularly well-suited for outlier detection. This is due to its wide dynamic range and reliance on electrical impedance to individually count and size particles suspended in dilute conducting liquids. Originally developed to count blood cells, the technique is now applied in numerous and varied industries and scientific fields. Examples of successful application of the Coulter Principle include characterisation of: ink toners, plant cells, abrasive grit, chromatography media, protein aggregates, in-vitro diagnostic beads, rocket fuel, and ocean plankton.
The key differentiator of the Coulter Principle from other particle sizing technologies is that each particle is individually analysed, and thousands to millions of particles can be analysed in a single run. This gives the technique a very high resolution and a wide dynamic range. In the best current implementation, particles that vary as much as 30-fold in diameter can be measured in a single test. While other techniques such as laser diffraction have wider dynamic ranges, few have the ability to individually count particles.
Thus, if the largest particles in a sample are at vanishingly low concentrations, while the main particles are much smaller and at high concentrations, many techniques will “miss” the larger particles. Conversely, particle sizing technologies relying on detecting the intensity of scattered light—such as laser diffraction and dynamic light scattering—are unable to pick up even relatively high concentrations of smaller outliers because of the sixth power relationship between particle diameter and scattered light intensity. In essence, the signal from the highly concentrated particles will overwhelm the low concentration particles. There are many excellent references that provide a detailed scientific description of the Coulter Principle and example applications.1-2
One limitation of the Coulter Principle is the need for a dilute conducting liquid. “Dilute” refers to the particle concentration. If the particle concentration is very high, it becomes impossible to ensure that particles are measured individually. Generally, this refers to particles within the dynamic range of the measurement. The overall dynamic range of the best available COULTER COUNTER is 0.200 to 1600 microns; but each individual measurement’s dynamic range is dictated by the aperture (a small orifice through which liquid, particles, and electrical current pass during measurement) chosen and the size of the particle being analysed. For example, if the measurement is made with a standard 100-μm diameter aperture of 2.0-μm particles, the ideal concentration that ensures one particle at a time passes through the aperture is ~64,000 particles/volume. For each given aperture, particles are too small to be detected above background noise if their diameters are smaller than 2% of the aperture diameter, while particles with diameters larger than 60% of the aperture diameter start to produce nonlinear electrical signals due to wall effects within the aperture. Thus, it is important to have a rough estimate, within two orders of magnitude, of the size of the particles being analysed ahead of time to prevent aperture clogging.
An interesting and novel problem occurs when there are very high concentrations of particles smaller than the lower-end of the dynamic range, but the particles of interest are within the dynamic range of the aperture. For example, in a typical CMP slurry, particles are 10 to 20 nm in size, and manufacturers are concerned with eliminating particles that are much larger (e.g., 400+ nm in size). An identical problem can occur in many other industries as well, such as ink toner manufacturing and medical devices, and can be called “outlier detection”—finding one large particle in a suspension of highly concentrated small particles.
Experimental DesignTo test whether the Coulter Principle could be used in this environment, a model system was devised which consisted of:
— Ludox HS-40 (Sigma Aldrich), which is a 40 wt% suspension of colloidal silica particles approximately 20 nm in diameter;
— Beckman Coulter L1000, which is a suspension of latex beads with a nominal 1.0 μm diameter; and
— Beckman Coulter L10, which is a suspension of latex beads with a nominal 10 μm diameter.
The 1.0-micron particles act as the large outlier contaminant in the Ludox system; in another experiment, the 1.0-micron particles act as a smaller contaminant in a solution of 10-micron beads. 0.1 M sodium triphosphate buffer was used as a diluent due to its previously proven ability to dilute Ludox stably. A series of experiments—utilising a 20 μm aperture (dynamic range of 0.400 to 16 μm) installed on a Multisizer 4 instrument—were designed to probe the model system.
The first set of studies was to determine whether or not background signals would be generated by the highly concentrated Ludox suspensions. For this test, the stock-concentrated Ludox was diluted to concentrations ranging from 3 wt% to 15 wt% solid. The hypothesis driving these experiments was that highly concentrated particles could cause enough disruption in electrical current to produce a background signal, which should increase with time.
The next set of experiments served as proof of principle to determine whether or not 1.0-micron particles could be detected above background of the same highly concentrated Ludox suspensions (6.0 wt%) used in the first experimental set. For the positive test case, one drop of Beckman Coulter L1000 standard was added to each of the same vials used for background measurements.
The third round of experiments aimed to determine whether or not the 1.0-micron particle concentration could be quantitatively assessed above background. To accomplish this, a stock solution of 6.0 wt% Ludox in 10 mL of sodium triphosphate buffer was prepared and mixed with either 50 or 100 μL of L1000 1-micron beads. The experiment was run in volumetric mode (50 μL), so that the total concentration of L1000 beads/mL could be calculated.
The final round of experiments focused on multiple outlier detection; while the Coulter Principle is more adept at detecting small amounts of large outliers than typical light scattering techniques, it is vastly superior over any other technique at detecting low amounts of smaller outliers. The differentiating power of the Coulter Principle is demonstrated by making a solution with 1:10,000 dilution of 1-micron beads, and 1:1,000 dilution of 10-micron beads. Thus, the 10-micron beads are roughly an order of magnitude more concentrated than the smaller 1-micron beads. The dual outliers were analysed in series of mixtures with and without Ludox to assess the influence of the concentrated background particles on small outlier detection.
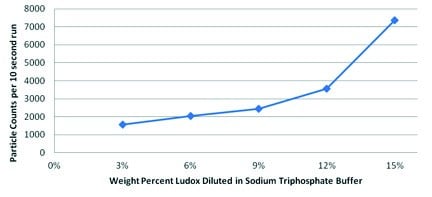
ResultsFigure 1 shows that background noise (in the form of particulate counts) was indeed observable and increased with concentration of Ludox. This phenomenon may occur because the particles themselves displace conductive liquid inside of an aperture, resulting in such high concentrations that these displacements are measurable. The nonlinear nature of the signal increase likely relates to the volume occupied by ever-larger numbers of particles. Despite this background noise, the absolute level of background counts was relatively low and stable.
The second experiment aimed to determine whether or not particles could be detected accurately above these backgrounds. Figure 2 shows the results of these tests. The data in this graph represents the average of two runs per dilution. The variation in counts is likely due to sample preparation error (droplet size is difficult to control and is not standardised).
One difficulty in this test was that highly concentrated Ludox tends to coat all glass surfaces it contacts; excellent cleaning procedures and sample handling were necessary. Also, this practically limited the upper-end of the experimental data set to 15 wt% Ludox, because at higher concentrations, the aperture became clogged with the small nanoparticles. It could not be determined whether this characteristic was a result of unique Ludox chemistry, or more likely, if it simply resulted from the very high solid concentrations. Still, this data clearly demonstrates the ability of the Coulter Principle to accurately and reproducibly detect large outlier s in highly concentrated suspensions of small particles.
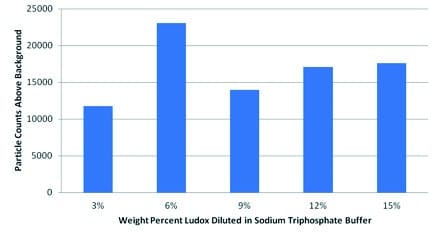
The third experimental data set, shown in Figure 3, proved that particles suspended in highly concentrated Ludox could be accurately detected in proportion with their concentration. At 1:200 dilution, an average of 54,900 particles was counted (ranging from 0.4 μm to 12 μm) in 50 μL of analysed sample; at 1:100 dilution, an average of 104,600 particles were counted. In all trials, the mean particle diameter was 1.084 to 1.098 micron, while the median particle diameter was 1.064 to 1.070 micron. Thus, even with a huge excess of Ludox, the Multisizer is able to quantitatively determine the concentration of larger outlier contaminants.
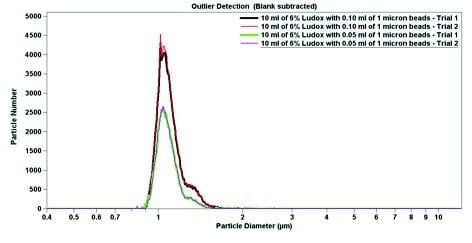
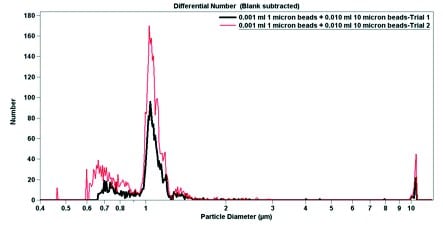
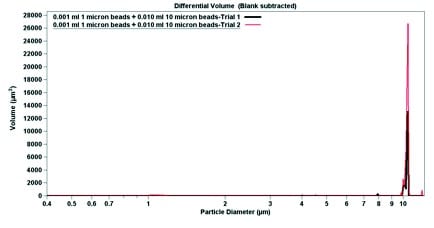
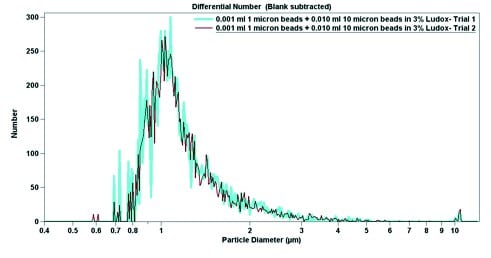
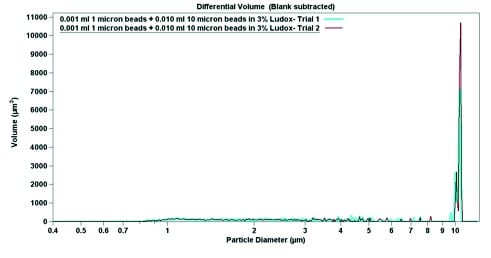
The final experimental data is shown in Figure 4. Using pure sodium triphosphate buffer and 6.0 wt% Ludox, both 1.0-micron particles and 10-micron particles were suspended. In pure buffer, the 1.0-micron particles have a narrow peak (Figure 4), which broadens when the particles are mixed with Ludox (Figure 5). In both cases, despite a large excess of 10-micron beads (roughly 10-fold), the 1-micron beads are easily detectable. When par ticle diameter is plotted against volume, the 10-micron beads dominate; a small but detectable signal can be seen near 1 micron (Figures 4b and 5b). Contrastingly, when the particle diameter is plotted against particle number, the smaller but more numerous 1-micron beads dominate the signal (Figures 4a and 5a). The data from Figure 4 indicates that the Multisizer 4 is able to pick up small outliers from the main distribution, while the data from Figure 5 displays how the Multisizer 4 is able to pick up several distributions of larger outliers.
DiscussionThe data presented here clearly shows that the Coulter Principle, as implemented in the Multisizer 4, is a powerful and capable tool for monitoring outliers— even in extremely concentrated solutions. The instrument proved capable of detecting extremely low concentrations of large particles mixed with very high concentrations of small particles. Some expected nonlinear behaviour was observed due to the unique sample characteristics. However, this signal is reproducible and can be removed through careful experimental design and background subtraction.
While this data set focused on a system designed to mimic CMP slurries, it proves a point which is more broadly applicable to the Coulter Principle: the Multisizer Series is capable of detecting very low concentrations of outliers, both larger and smaller than the main distribution. The key properties of the Coulter Principle that endow it with this ability are the broad dynamic range (up to 30:1 by diameter ratio), the ability to count individual particles, and very high sensitivity. For these reasons, the Coulter Principle has many advantages over ensemble techniques based on light obscuration or scattering, which analyse whole populations at once and would have difficulty detecting low concentrations of large particles.
1. Coulter, W H. Means for Counting Particles Suspended in a Fluid. U.S. Patent 2,656,508. October 20, 1953.
2. Graham, M D. The Coulter Principle: Foundation of Industry. Journal of the Association for Laboratory Automation. 8 (6); 72–81: (2003).
3. Hanus, L et al. Optimizing the sizing and counting accuracy of CMP slurry large-particle counts. Micro Magazine. (March 2006).
More information
More information on the Beckman Coulter Multisizer 4e here.